粒子群优化算法

在学海之中种下的浮标，记录自己学习的成果。看完了各种博客对粒子群优化算法的介绍，并结合具体问题写写代码，总结一下学习笔记，于人于己都是善举吧。

一、粒子群算法的简介

　　粒子群优化（Particle Swarm Optimization, PSO），又称微粒群算法，是由J. Kennedy和R. C.Eberhart等于1995年开发的一种演化计算技术，来源于对一个简化社会模型的模拟。其中“群（swarm）”来源于微粒群符合M. M. Millonas在开发应用于人工生命（artificial life）的模型时所提出的群体智能的5个基本原则。“粒子（particle）”是一个折衷的选择，因为既需要将群体中的成员描述为没有质量、没有体积的，同时也需要描述它的速度和加速状态。
　　PSO算法最初是为了图形化的模拟鸟群优美而不可预测的运动。而通过对动物社会行为的观察，发现在群体中对信息的社会共享提供一个演化的优势，并以此作为开发算法的基础。通过加入近邻的速度匹配、并考虑了多维搜索和根据距离的加速，形成了PSO的最初版本。之后引入了惯性权重w来更好的控制开发（exploitation）和探索（exploration），形成了标准版本。为了提高粒群算法的性能和实用性，中山大学、（英国）格拉斯哥大学等又开发了自适应（Adaptive PSO）版本和离散（discrete）版本。 –维基百科

1. 粒子群算法的问题提出：

　　设想一个场景：一群鸟在随机的搜索食物，在这个区域里面只有一块食物，但是鸟群里所有的鸟都不知道食物的具体地址在哪里，但是它们知道自己当前的位置距离食物还有多远的距离。那么，找到食物的最优策略是什么呢？最简单有效的方法就是搜索目前距离食物最近的鸟的周围区域。

2. 问题抽象求解：

　　将鸟抽象成没有质量和体积的微粒（点），并将该点延伸到N维空间（用于解决多目标优化问题）。对粒子i在N维空间的位置表示为矢量：$X_i = (x_1,x_2,…,x_N)$, 飞行速度表示为矢量：$V_i=(v_1,v_2,…,v_N)$. 每个粒子都有一个由目标函数决定的适应值$FitnessValue$，并且知道自己到目前位置发现的最好位置($Pbest$)和现在的位置$X_i$。这个可以看作是粒子自己的飞行经验。而且，每个粒子都知道目前位置，整个群体里面的最好位置（$Gbest$）,这个可以看作是粒子同伴的经验。粒子就是通过自己的经验以及和同伴之间的交流来决定下一步的运动的。

3. 粒子群算法的算法原理

粒子群算法的基本步骤主要为：

• 初始化粒子种群，产生一组随机解；
• 计算在初始解的情况下，每个粒子自生的经验最优Pbest和全局最优Gbest，并计算各个粒子的适应度；
• 根据公式1更新每个粒子的速度；
• 根据公式2更新每个粒子的位置；
• 计算每个粒子的适应度；
• 更新每个粒子的经验最优Pbest和全局最优Gbest；
• 直到循环终止条件达到。

算法的过程中，更新各个粒子的位置和速度的公式如下：
$$V_i=\omega \times V_i+c_1\times rand()\times (Pbest_i-X_i)\
+c_2\times rand()\times (Gbest-X_i)$$
$$X_i=X_i+V_i$$

　　在公式（1）中，$\omega$为惯性权重(inertia weight)，C1和C2为加速常数，rand()为在[0,1]范围内变化的随机值。对于速度$Vi$，其被一个最大速度$V{max}$所限制，如果当前粒子的某一维度的速度超过该维度最大速度$V{max}$，则该维度的速度被限制为该维最大速度$V{max}$。

　　对于公式（1）,可以将其分为三个部分，第一个部分为微粒先前行为的惯性，第二部分为“先知”部分，表示微粒本身的思考，即粒子自己的飞行经验；第三部分为“社会”部分，表示微粒间的信息共享与相互合作。

二、粒子群算法的代码演示

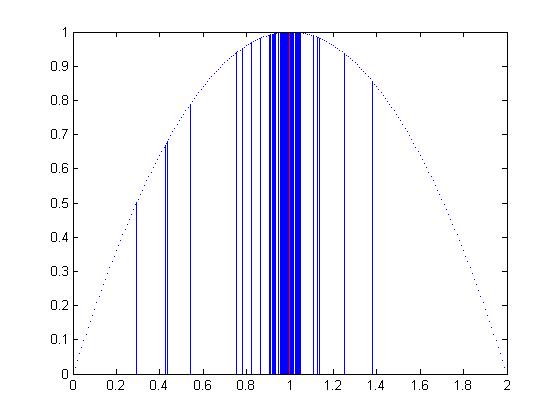
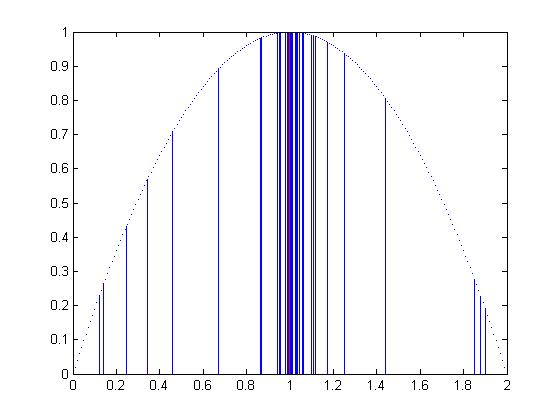
​ 现学现用，通过一个小例子，来验证自己对粒子群优化算法的理解程度。本例使用的是基本粒子群优化算法对实例进行求解，实例为：在[0-2]的区间内，求解函数$y=1-(x-1)^2$的最大值。显然，该问题的适应度函数为$max f(x) = 1-(x-1)^2$，并根据适应度函数，求解最优解。源代码如下：

clc;
for x=0:0.01:2
    y=1-(x-1)^2;
    plot(x,y);
    hold on;
end;
w = 0.4;          %惯性系数
c1 = 2;           %
c2 = 2;           %
Vmax = 0.1;
x1 = 0;     %随机点1的位置和速度
v1 = 0.01;
x2 = 2;    %随机点2的位置和速度
v2 = 0.02;
f1 = fitness(x1);
f2 = fitness(x2);
Pbest1 = x1;
Pbest2 = x2;
Gbest = compare(x1,x2);

%下面开始循环更新
for j=1:1000
    v1 = w*v1 + c1*rand()*(Pbest1-x1)+c2*rand()*(Gbest-x1);
    x1 = x1 + v1;
    if(x1 > 2) 
        x1 = 2;
    end
    if(x1 < 0)
        x1 = 0;
    end
    v2 = w*v2 + c1*rand()*(Pbest2-x2)+c2*rand()*(Gbest-x2);
    x2 = x2 + v2;
     if(x2 > 2) 
        x2 = 2;
    end
    if(x2 < 0)
        x2 = 0;
    end
    %更新适应度值
    f1 = fitness(x1);
    f2 = fitness(x2);
    line([x1,x1],[0,f1]);
    line([x2,x2],[0,f2]);
    Pbest1 = compare(Pbest1,x1);
    Pbest2 = compare(Pbest2,x2);
    Gbest = compare(Gbest,Pbest1);
    Gbest = compare(Gbest,Pbest2);
    %plot(Gbest,fitness(Gbest),'g');
end 
f = fitness(Gbest);
line([Gbest,Gbest],[0,f],'color','r');

其中用到的函数分别为compare和fitness函数，其源码分别为：

function fitnessValue = fitness(x)
%计算每个点的适应度值，在本例中，每个点的适应度值为x点处的y值
% 计算公式为：y=1-cos(3*x)*exp(-x)
fitnessValue = 1-(x-1)^2;

function maxValue = compare(a,b)
t1 = fitness(a);
t2 = fitness(b);
if(t1>t2)
    maxValue = a;
else
    maxValue = b;
end

mablab的运行结果为（运行了两次，因为算法中运用了随机函数，因此两次的运行结果不一样，但是计算的最优位置保持一致，其中红色的线表明最优位置）：